wordpress 导航菜单 居中seo外包网络公司

1. 题目理解

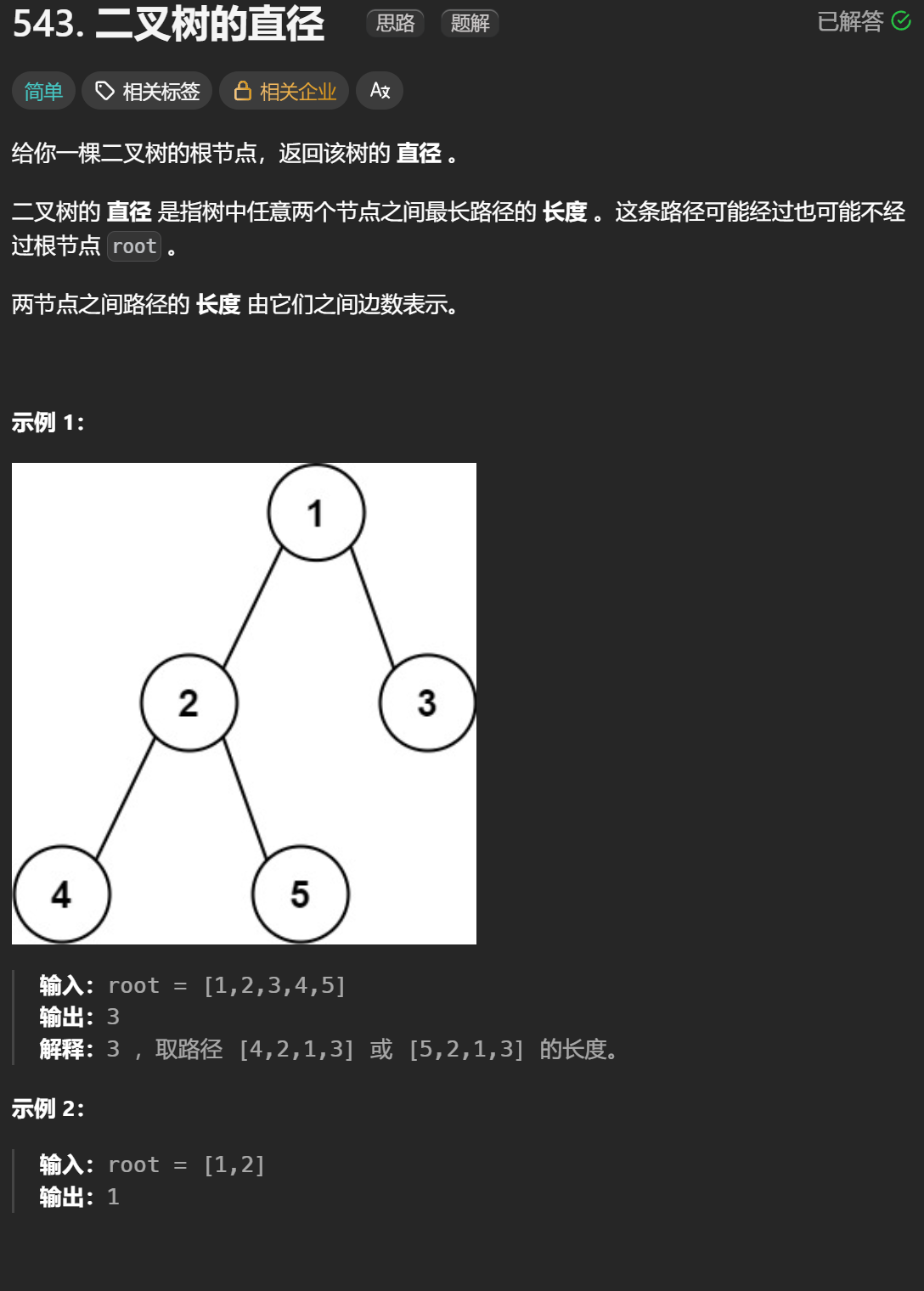
• 定义：二叉树的直径是树中任意两个节点之间最长路径的长度（边数）。
• 这条最长路径可能经过根节点，也可能不经过。
• 注意：直径的长度是边数，而递归中常用的深度是节点数。

例如：

    1/ \2   3/ \
4   5

• 直径 = 3
  路径：4 -> 2 -> 1 -> 3，共 3 条边。

2. 解题思路

要找二叉树直径，可以这样分析：

2.1 关键观察

对于任意一个节点 root：

• 经过该节点的最长路径长度 = 左子树最大深度 + 右子树最大深度
• 所以我们只需要遍历所有节点，计算每个节点的最长路径长度，取最大值即可。

2.2 递归策略

• 采用后序遍历（先算左右子树，再算当前节点），因为要先知道左右子树的深度才能算直径。
• 在递归计算深度的同时，顺便更新全局变量 maxDiameter。

2.3 为什么返回深度而不是直径？

• 父节点的直径需要通过子树深度计算：

  父节点直径 = 左子树深度 + 右子树深度
  

• 如果递归返回直径而不是深度，父节点就无法正确计算自己的直径。

3. 代码解析

class Solution {// 全局变量，用于记录最大直径int maxDiameter = 0;public:int diameterOfBinaryTree(TreeNode* root) {maxDepth(root);  // 递归计算深度的同时更新 maxDiameterreturn maxDiameter;}// 返回以 root 为根节点的最大深度（节点数）int maxDepth(TreeNode* root) {if (root == nullptr) {return 0; // 空节点深度为 0}// 递归计算左右子树的最大深度int leftMax = maxDepth(root->left);int rightMax = maxDepth(root->right);// 经过当前节点的直径 = 左子树深度 + 右子树深度int myDiameter = leftMax + rightMax;// 更新全局最大直径maxDiameter = max(maxDiameter, myDiameter);// 返回当前节点的最大深度return 1 + max(leftMax, rightMax);}
};

4. 复杂度分析

• 时间复杂度：O(n)
  每个节点只被访问一次。
• 空间复杂度：O(h)
  递归栈的深度，h 为树的高度，最坏情况下 O(n)。